はじめに

MR認定試験、精度管理の鬼門、スライス厚測定です。
これのせいで受験のハードルが爆上がりです。

なんといっても、ファントムがないと始まらないです。

しかし私はファントムを自作する術（外注ですが(‘_’)）を編み出しました。
これで受験できます。
では測定。

ファントムを用意

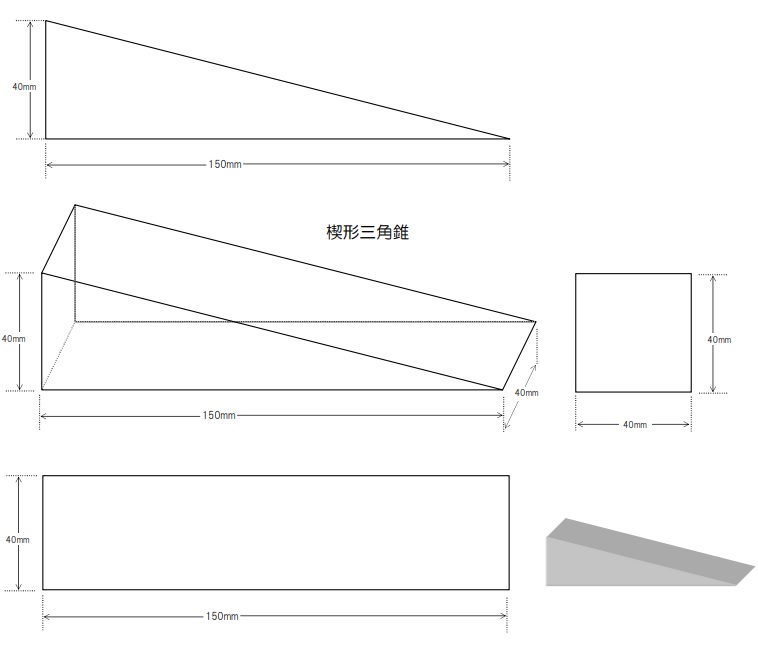
まずは撮影対象となるファントムが必要です。

MRI装置付属ファントムにスライス厚用があって、形やサイズが条件に合っていればOKです。
無い方は借りるか、作るか、が必要です。

日興ファインズ工業（現 本橋化成工業）のファントムが有名ですね。
解説本などはだいたいこれです。
職場で買っていただける場合はぜひ。
MRIファントム.JP | 有限会社本橋化成工業 (mri-phantom.jp)

ファントム製作（外注）のしかた

別の記事にしましたので、どうぞ。
私の書いた上のファントム製図を使用してください。

スライス厚測定用ファントム製作（外注） | 磁気共鳴専門技術者認定試験にチャレンジ！ (brightwalk.net)

ファントムの条件

１）標準的なNEMA法に準じて、ウェッジ法を用いて測定を行う。
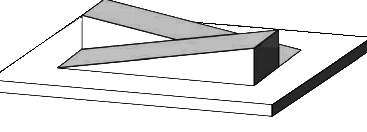
２）2枚の楔型三角錐が交叉したスライス厚測定用ファントムの使用が望ましい。
３）撮像条件
　　・SE法を用い、マルチスライスで撮像を行う。
　　・マルチスライスで少なくとも3スライスは撮像を行い、スライス間距離が予想される半値幅の2倍以上であること。
　　・TR≧3×T1、スライス厚とTEは一般的に臨床に使用される範囲。
　　・十分なSNRを担保すること。
４）測定に際しコンピュータソフトを使用してもいいが、結果は正方眼紙1枚に測定方法とともに、得た数値の根拠となる計算式を表示する。
５）楔形三角錐がひとつしかない場合や、当該ファントムを持ち合わせていない場合は、ファントムを作成もしくは独自な方法で求めてもよい。独自な方法を用いる場合は、信頼度を記す。

性能評価試験項目｜日本磁気共鳴専門技術者認定機構(JMRTS) (umin.ac.jp)より引用

素直に楔型三角錐が交叉したファントムを用意します。
 

ファントムの設置

ファントムが手に入ったら、ファントムを固定します。ずれがないようにしっかり固定です。
そして溶液とファントムが入る程度の箱（タッパーなど）に入れます。
箱に入ったら溶液を注ぎます。

溶液はなんでもよいと思います。
【TR1000-2000/TE15‐100】の条件下で高信号になる溶液です。
いろいろ試してみるのが楽しいと思います。

ちなみに私は洗濯糊のPVAで試しました。既成ファントムがPVAを使用しているからです。
思いっきり失敗しました。
時間がある方はぜひ試してみて下さい。

カネヨ石鹸 PVA 洗濯のり カネヨノール 液体 750ml スライム作り

https://amzn.to/3OGN80Z

amzn.to

撮影条件

・SE法を用い、マルチスライスで撮像を行う。
・マルチスライスで少なくとも3スライスは撮像を行い、スライス間距離が予想される半値幅の2倍以上であること。
・TR≧3×T1、スライス厚とTEは一般的に臨床に使用される範囲。
・十分なSNRを担保すること。

性能評価試験項目｜日本磁気共鳴専門技術者認定機構(JMRTS) (umin.ac.jp)より引用

注意点

書いていて思ったのですが、
アキシャルでの撮影の条件があった気がするのですが、違ったでしょうか？
NEMA？

アキシャルでの条件が無いとすると、かなり楽です。

This standards publication provides a method for determining the slice thickness of proton images.
Both the typical and the typically thinnest slices in routine clinical use for a particular system are determined at one location within the specification volume and at only one of the three orthogonal orientations (transverse, sagittal, or coronal). Imaging types and conditions not addressed by this standard include spectroscopy, chemical shift imaging, and warped slices.

NEMA MS 5 DETERMINATION OF SLICE THICKNESS INDIAGNOSTIC MAGNETIC RESONANCE IMAGINGより引用

NEMA資料では、断面に関する記述はここだけでした。
とりあえず、どの断面でもよさそうです。オブリークはだめって感じですね。
真面目にやるとしたら、均一試験のように、３断面分のスライス厚誤差を測定するのかな。

撮影

参考条件

注意点

・スライス間距離をスライス厚と同等にする。
・”TR≧3×T1″とあるので実際に測定した値より長めに設定する。
・FOVは256mm、マトリックスを256*256にすると後で計算しやすい。
・加算回数を可能な限り多くする。
・スライス厚は“一般的に臨床に使用される範囲”とある。普段よく撮影しているスライス厚などでOK。
　NEMAでは、”⽇常的な臨床使⽤における典型的なものと最も薄いものの両⽅”と規定している。
・位置決めスキャンをかなり慎重に行う。
　位置決めスキャンを何度も何度も行い、目視でのズレが全くないまで精度を良くして撮影。

SCAN

撮影した画像です。若干斜めになっています。
10回程度ずれを直してもこうなってしまいます。あきらめます。

何度やっても斜めになってしまった場合、そのままで解析に進みます。
多少斜めでも、一番最後に回転補正という、斜め補正を行うので問題無いです。

ImageJで解析

撮影が終了したら解析です。
DICOM形式で画像をとりだし、ImageJに読み込ませます。

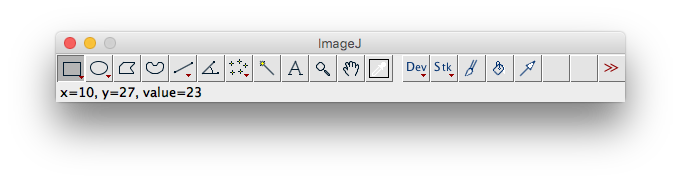
ImageJに画像を読み込み、上のくさびの移行部分にROIを取ります。
ROIをとったら【Image】▶︎【Duplicate…】をクリックし、移行部分のみを切り取ります。

これを上下の移行部分に対して行います。

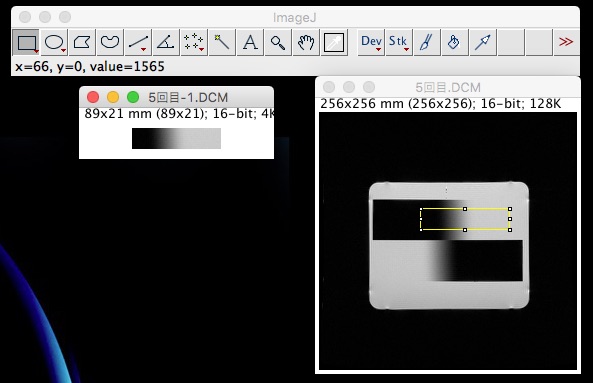
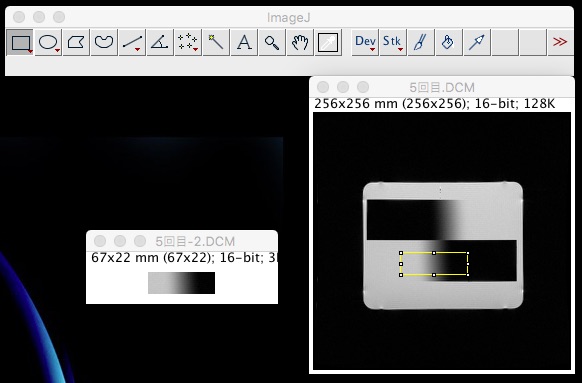
次にこの画像を数値に置き換えます。
ImageJのメニューより、【 File】▶︎【Save as】▶︎【Text Image…】にて保存します。

 

テキストデータが作成されました。

これを上下のくさび２つに対して行います。

 

Excelで解析

次はExcelでの作業です。

エクセルに先ほどのデータを読み込ませます。

エクセルの【File】▶︎【開く】で先ほど作成したText dataを指定します。

上下のくさび同時にはできないのでどちらかから行います。
まず上のくさびから行います。（第一くさびとします。）

 

すると画像をどう開くか？と聞かれるので、区切り記号付き、タブとスペースにチェックを入れます。

Excelに読み込まれました。
 

データより、グラフを作成します。
まず、列ごとに平均値をとります。

ExcelのΣマークから平均を選択し、平均値を算出します。

平均値が算出されました。

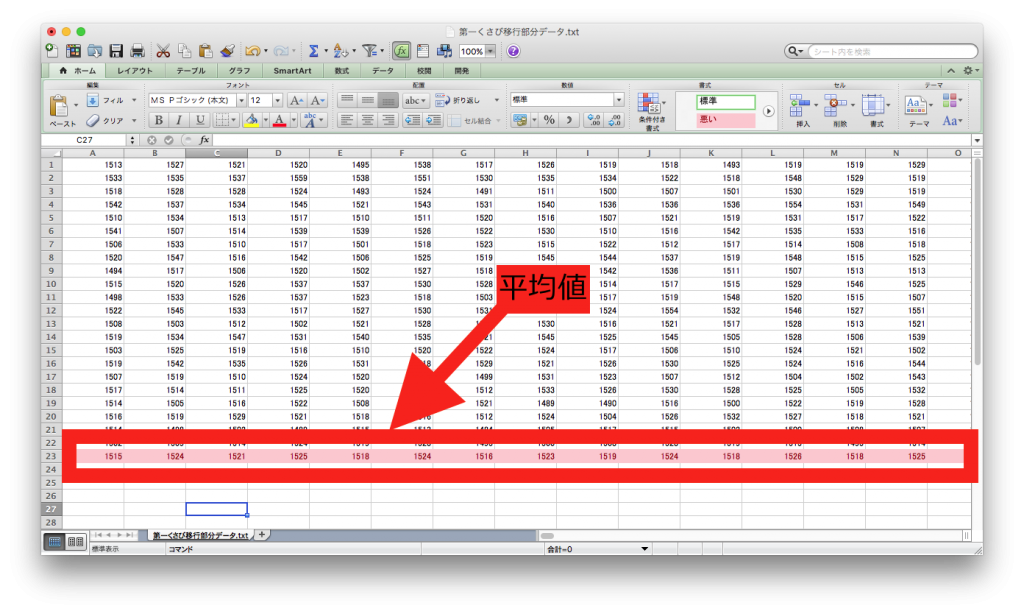
次は、算出した平均値より、差分をとります。
隣同士のセルを引き算します。
画像では、1524-1515をA24のセルに計算式として入力しています。

全列に適応していきます。

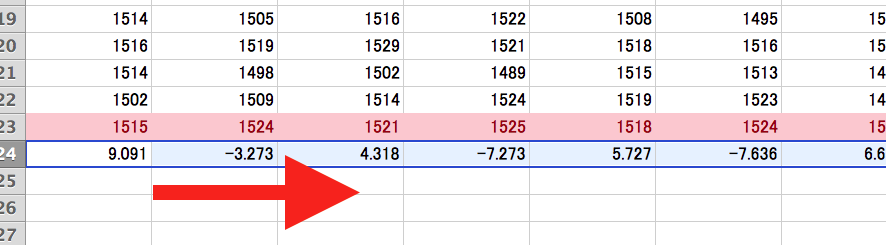
差分値よりグラフを作ります。
マーカー付き折れ線グラフが見易かったです。おすすめ。

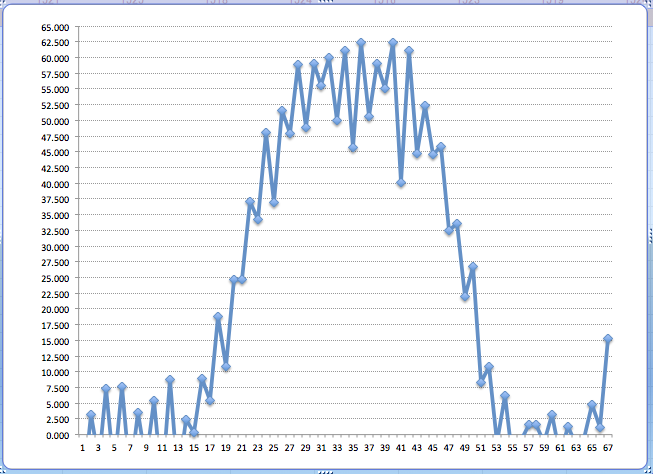
第一くさびのスライスプロファイルのグラフが完成しました。

グラフが逆になっていませんか？
差分する順がちがうはずです。

 

このグラフを第二くさびも行います。

計算

得られた２つのグラフより、スライス厚を求めていきます。

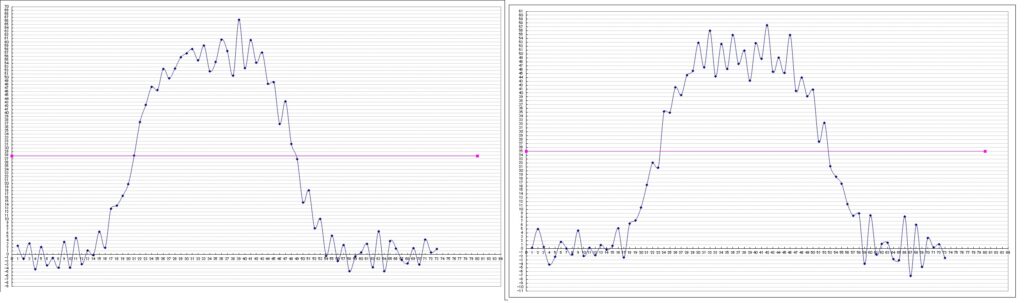
計算順序

グラフが作成できたら、グラフから読み取れるデータを得ていきます。
そしてそのデータを使用して計算します。

１．平均信号最大値、最小値を測定

まずグラフをプリントアウトするか、正方眼紙に書きます。

Bitly

amzn.to

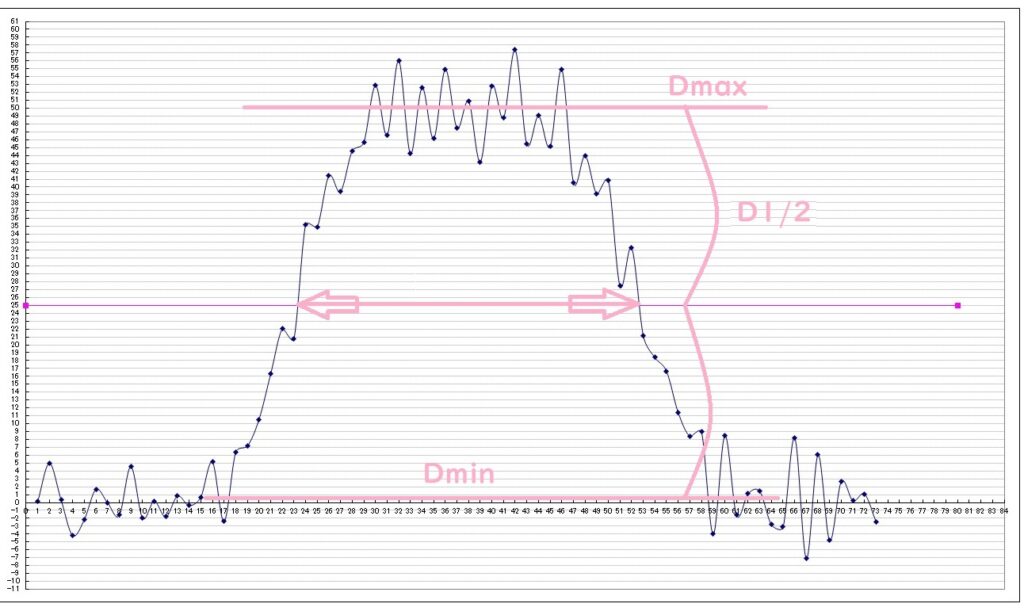
平均信号最大値の算出（Dmax）
グラフより、信号が高い平坦部分の平均をとります。
平坦部分と思われる点、例えば１２点ほどが平坦部分と言える場合、その１２点の平均値です。
６点以上はとるようにしてくださいね。NEMAの測定方法です。

2.2.2 Measurement Procedure
Select the acquisition and display parameters so that the resulting spatial resolution in the x direction　(see Figure 2-3) is sufficient to include at least six “intrinsic” pixels across the FWHM of the stretched　(projected) slice profile. For the purposes of this standard, the “intrinsic” pixel size is defined as the　image domain distance d (in meters) such that 1/d (in meters-1) is the span of the measured data in　the Fourier domain. An example is shown in the Authorized Engineering Information below. This
condition is met when:（後略）

NEMA MS 5 DETERMINATION OF SLICE THICKNESS INDIAGNOSTIC MAGNETIC RESONANCE IMAGINGより引用

平均信号最小値の算出（Dmin）
次に最小値です。信号が低い平坦部分の平均をとります。
低信号部分は左右にあるため、左右の平均をとります。

ここでの平均値の算出は、エクセルにあるデータで平均値を計算した方が早いかもしれませんね。
ただ、フィーリングでやってもOKだと思いますｗ

今回は例としてこの値を使っていきます。

２．半値幅(D1/2)の測定、ピクセル数 算出

半値幅(D1/2)を算出していきます。

だったので、

半値幅(D1/2)が算出できました。

次はピクセル数の算出です。

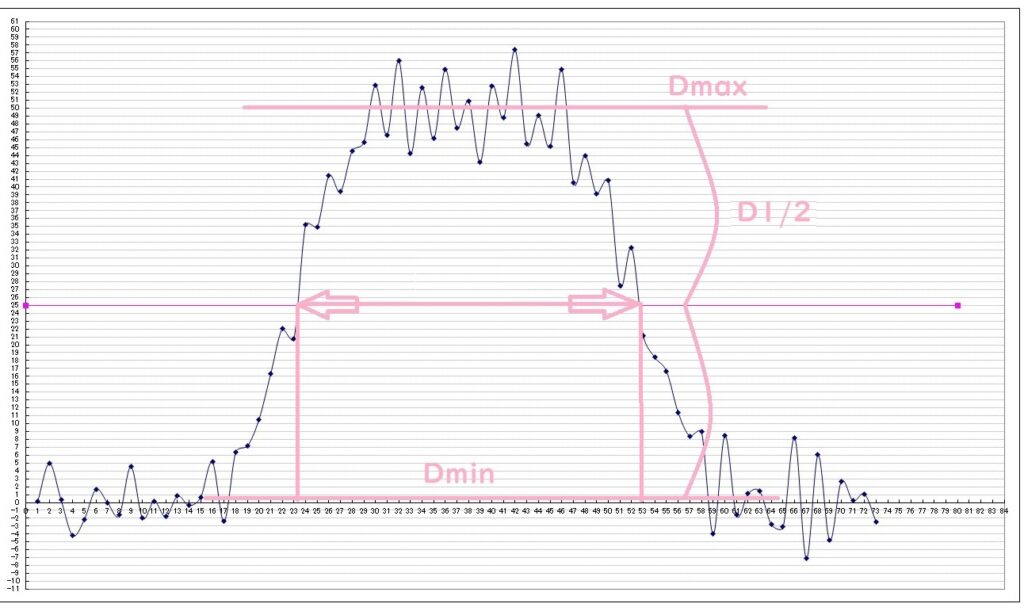
半値幅（D1/2）のところで線を引きます。（真ん中のライン）
グラフの内側の部分のピクセル数を横軸から読み取ります。

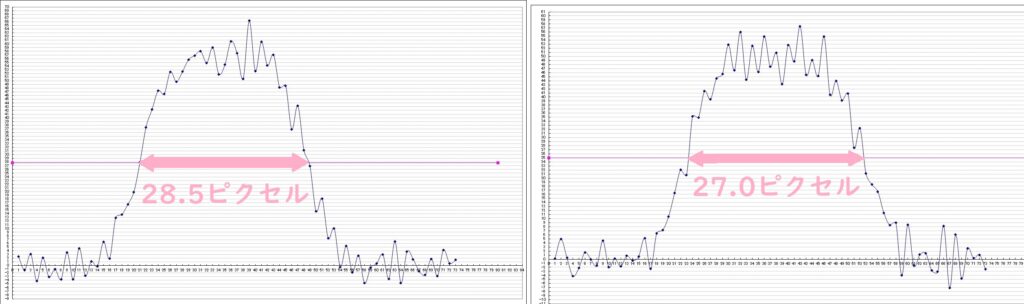
ピクセル数が読み取れました。

３．ピクセルサイズ算出

ピクセルサイズを計算します。
撮像条件よりFOV＝256mm、ﾏﾄﾘｯｸｽ数＝256*256、
よって　1ピクセルサイズ＝1mm

条件によってもちろん変わるので、各自計算してくださいね。
おすすめは、上記の[FOV＝256mm、ﾏﾄﾘｯｸｽ数＝256*256]が簡単です。

４．半値幅（ｗ）の算出

半値幅（ｗ）を求めます。
半値幅　ｗ=ピクセル数×１ピクセルサイズ で計算できます。
 
第一くさびをw1、
第二くさびをw2とすると

５．スライス厚算出

スライス厚は半値幅にくさびの角度tanθをかけて求めることができます。

三角関数の計算はこちらが早いです。

三角関数（度） – 高精度計算サイト (casio.jp)

私が作成したファントムはtanθ=14.25°です。
使用したファントムによってもちろん角度は異なるので注意してくださいね。

スライス厚の測定は無事終了です。
しかし、くさびの1と2でスライス厚が違ってしまっています。

これを補正しなくていけません。
次は回転補正の計算です。

6.回転補正

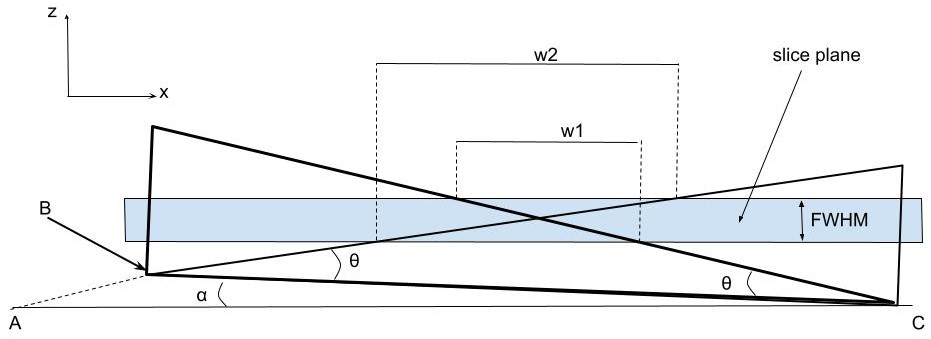
撮像断面の平行の軸に対しての回転補正を行い、真のスライス厚を求めていきます。

理論

座標軸は３つあるので、撮影時に３次元的にずれてしまい、それが原因でスライス厚の誤差になります。
上図を確認してください。
z軸を中心に回転してしまうと、画像全体が回転するのがわかると思います。
ｙ軸を中心として回転してしまうと、くさびの角度が直接変わってしまうため、誤差が大きくなります。
今回のスライス厚の補正にはこのy軸の誤差補正が必要になります。

ｙ軸を中心とした回転誤差を求める式は以下で表せます。

αは、回転誤差です。図を参照してください。
θはくさびの角度です。

誤差角度αの計算

測定結果から代入していきます。

三角関数の計算はこちらが早いです。

三角関数（度） – 高精度計算サイト (casio.jp)

真のスライス厚の計算

測定された第一くさび半値幅(w1)、第一くさび半値幅(w2)は,
それぞれ傾斜角(θ-α)、(θ+α)のウェッジにてスライス厚を測定したことに等しいため、　　　　　　　以下の２つの式が導かれます。

これらより傾斜角を導きます。
実際に計算していきます。

αが求まったので、補正されたスライス厚を算出します。
求めたαを式（１）に代入します。
今回使用したファントムの角度は14.25度なので、

よって回転補正後のスライス厚は7.04ｍｍ です。

 

まとめ

グラフがちょっと歪すぎるグラフでしたね。
もう少しSNRを良くしたり、まっすぐ撮影することによって、グラフも良くなっていくと思います。
計算しやすいようにFOVやマトリックスを256にしてしまったのも要因だと思います。
今回は誤差0.04ｍｍとなってしまいましたが、もう少しちゃんとやれば良い精度で測定できるかもしれません。

レポートの書き方 | 磁気共鳴専門技術者認定試験にチャレンジ！ (brightwalk.net)

次はT１T2値測定です。